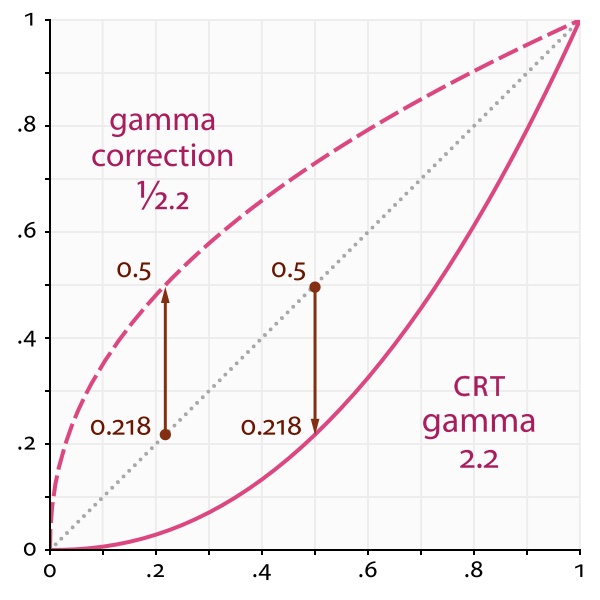
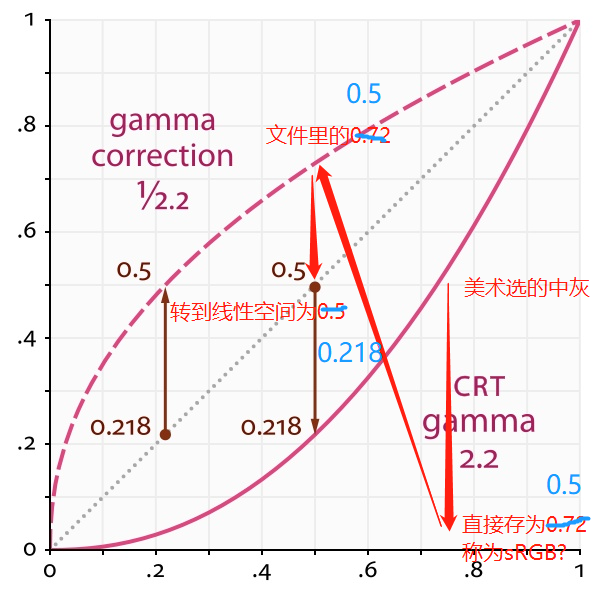
首先,我们来看一下这张图,其中 CRT gamma 曲线表示了老式CRT显示器中电压与亮度的关系,其中2.2为1953年确定的电视编码标准中的gamma值,接近大多数CRT显示器的原生gamma值,而现代 LCD 显示器已经不再具有这个特性,但是生产厂商仍旧会加入模拟 Gamma 曲线的硬件功能。gamma correction 曲线则是为了色彩正确显示而提出的gamma校正曲线,在图像保存时,颜色通常经过一次gamma校正以保存为一个较大数值,当显示时,由于显示器特性,会正好转换回校正前的物理亮度显示。
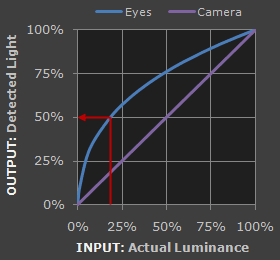
接下来,介绍一个重要的韦伯-费希纳定理(Weber-Fechner law),描述了物理刺激中的实际变化与感知变化之间的关系,即人眼对于亮度的感知是非线性的。
如下图所示,人眼对于暗部的感知更加精细,所以暗部亮度应当使用更细的精度保存。
结合这两点,HP与Microsoft 1996 年巧妙地结合了人眼感知的经验曲线与老式显示器的行业标准,选取gamma = 2.2的校正曲线,提出了sRGB color space,所以sRGB空间为gamma空间中应用最广泛的一种。

我们来看一下两种典型的中灰是如何被保存并进行光照计算与显示的。
第一种是物理亮度意义上的中灰,即物理亮度为0.5,也称为线性空间中的0.5灰。
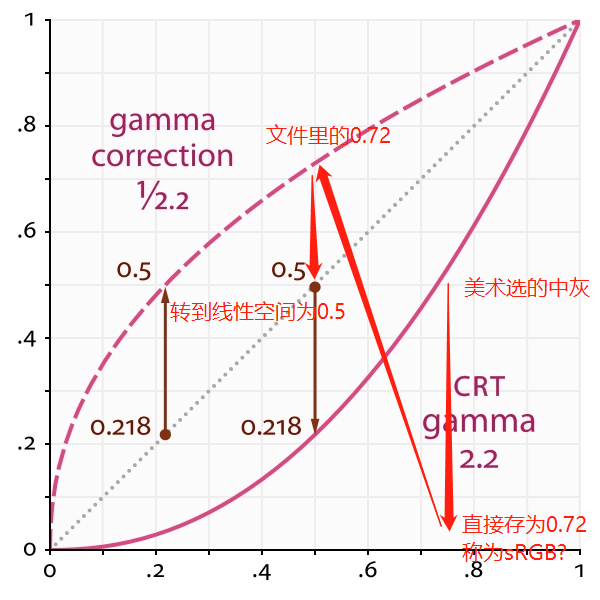
假设在线性空间下的调色版(如PS中32位/通道模式下的调色板)中,美术选取了值为0.5的灰色(并不是人眼感知的0.5灰),保存到sRGB空间时,会经过gamma校正保存为0.72。之后我们将其转换回线性空间值0.5进行光照计算,若光照计算后结果仍为0.5,那么我们转回sRGB空间继续保存为0.72。当显示器显示时,会将0.72作为输出电压(老式CRT显示器)或者进行CRT gamma模拟(现代LCD显示器),显示出0.5物理亮度的灰色。
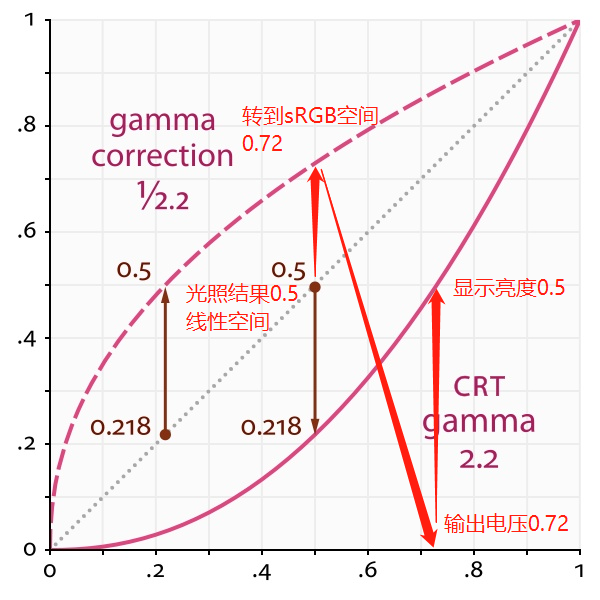
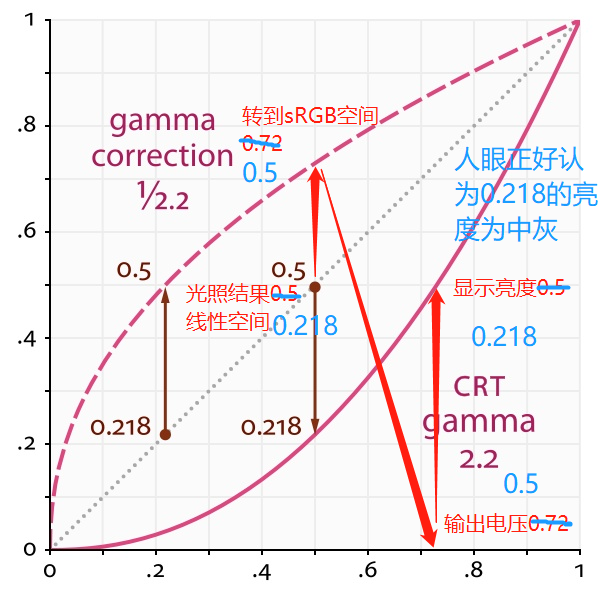
第二种是人眼感知意义上的中灰,即在人眼感知曲线上的灰度值为0.5,也称为sRGB空间中的0.5灰,实际物理亮度其实仅有0.218。
假设在sRGB空间下的调色版(如PS中8位/通道模式下的调色板)中,美术选取了值为0.5的灰色(也是人眼感知的0.5灰),保存到sRGB空间时,会直接保存为0.5。之后我们将其转换回线性空间0.218值进行光照计算,若光照计算后结果仍为0.218,那么我们转回sRGB空间会继续保存为0.5。当显示器显示时,会将0.5作为输出电压(老式CRT显示器)或者进行CRT gamma模拟(现代LCD显示器),显示出0.218物理亮度的灰色,而这个颜色正好是人眼感知的0.5中灰。
除了以上两种中灰,还有其他不同意义上的中灰,其物理亮度与sRGB值如下表所示。
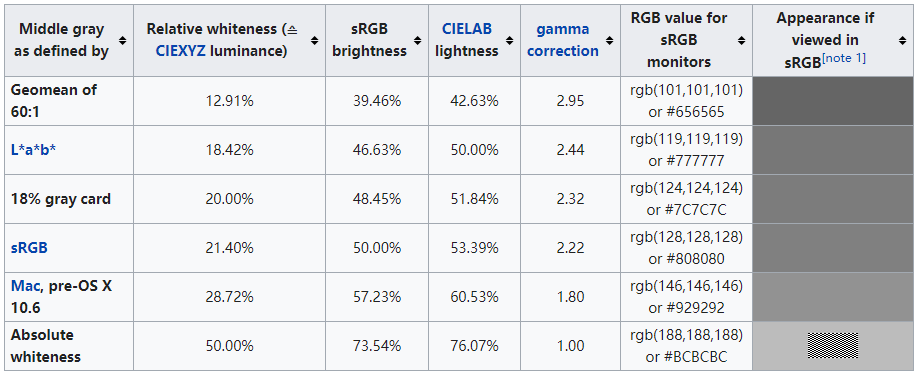
而之前详述的两种中灰分别为表中的Absolute whiteness与sRGB行
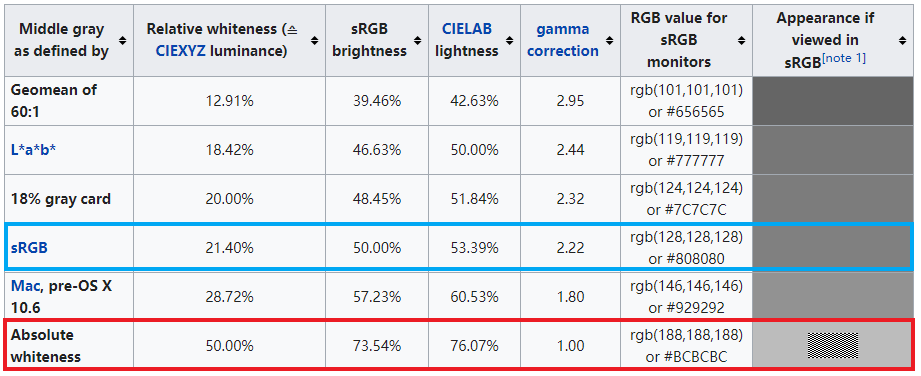
有趣的是Absolute whiteness行中的图中图放大后如下,黑色为0%,白色为100%时,下图平均物理亮度应为50%,而从远处看到与sRGB(188, 188, 188)的物理亮度完全一致,这使用Dither的方法证明了sRGB(188, 188, 188)的物理亮度确实是50%。

最终我们发现,之所以有sRGB色彩空间存在,其根本原因是人眼感知的经验曲线和 CRT 显示器的物理响应曲线能够基本吻合,而sRGB巧妙地将人眼感知的经验曲线设定为gamma = 2.2的gamma correction curve,兼顾了人眼感知精度与老式行业标准,不得不说这是一个美妙的Trick。